In questa guida spieghiamo come calcolare la pendenza di una salita.
Si tratta di un tema molto affascinante, oltre che importante. Questo valore, infatti, risulta essere decisivo quando cerchi di capire come affrontare le salite in bici. In questa fase è bene prepararsi per approcciare una salita in modo corretto. Nello specifico, il calcolo della pendenza ti serve per imparare a distribuire nel modo corretto le tue energie e le tue forze. Questa è una conoscenza che può esserti utile in circostanze diverse, e che dunque merita un approfondimento. Ecco perché è il caso di vedere cosa risulta essere e come si effettua il calcolo della pendenza di una salita.

In Cosa Consiste la Pendenza di una Salita
La pendenza, nota anche come gradiente, è un valore espresso in percentuale. Il valore indica il livello di inclinazione della strada rispetto ad un piano parallelo all’orizzonte. La pendenza parte sempre da un punto di inizio e termina presso un punto di arrivo. Tra i due punti, lunghezza del percorso, si ha un valore noto come dislivello. Il dislivello viene dato dalla differenza tra la quota altimetrica di arrivo e la quota altimetrica di partenza. Quando una strada è completamente piana, si dice che ha una pendenza pari allo 0%. Di contro, più si alza la percentuale di pendenza, più la salita viene considerata ripida. Se la strada è in discesa, si parla invece di gradiente o pendenza negativi.
Come Calcolare la Pendenza di una Salita
Per fare il calcolo della pendenza bisogna dividere il dislivello per la distanza percorsa e moltiplicare la cifra ottenuta per 100. Per capire meglio la situazione, prima di vedere un esempio pratico, puoi fare riferimento al grafico sottostante.
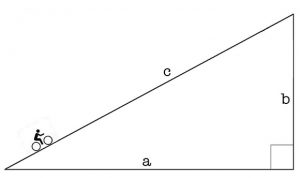
Risulta essere possibile spiegare meglio la situazione, facendo un esempio concreto. Mettiamo caso di dovere affrontare una salita lunga 5 chilometri, valore rappresentato da c nel grafico, con un dislivello di 350 metri, valore rappresentato da b nel grafico. La formula per calcolare il gradiente, come ti abbiamo anticipato poco sopra, è la seguente
(b/c) x 100
Di conseguenza, applicando i valori del nostro esempio, si ottiene il seguente risultato
(350/5000) x 100 = 7%
Il valore ottenuto con questa formula non è, però, completamente preciso. La pendenza effettiva andrebbe calcolata facendo il rapporto tra il dislivello, b, e la proiezione del tratto di salita sul piano dell’orizzonte, in pratica sul segmento a.
Se ci limitiamo a dividere 350 per 5000, in realtà stiamo dividendo il dislivello, b, per l’ipotenusa del triangolo, c, e non per a. Dunque abbiamo bisogno di trovare un modo per calcolare a. Per farlo dobbiamo utilizzare una formula matematica di base, che si studia alle superiori, si tratta del Teorema di Pitagora.
Il Teorema di Pitagora mostra la relazione tra le lunghezze dei lati di un triangolo rettangolo, e viene espresso dalla seguente formula
a² + b² = c²
Ricordati che c è la lunghezza dell’ipotenusa, e che a e b corrispondono ai due lati del triangolo. Noi conosciamo due di questi valori, c e b, e vogliamo scoprire il terzo a. Avendone due su tre, è possibile calcolare il dato mancante. I passaggi del calcolo sono i seguenti
a² + 350² = 5000²
a² + 122.500 = 25.000.000
a² = 25.000.000 – 122.500
a² = 24.877.500
Facendo la radice quadrata di a², otteniamo il valore finale di a:
a = 4988
Questo significa che affrontando una salita lunga 5 chilometri con un dislivello di 350 metri, abbiamo percorso esattamente 4988 metri in orizzontale. In sintesi, adesso conosciamo la distanza orizzontale percorsa, a. Questo ci consente di calcolare con esattezza il gradiente o pendenza della salita.
Quindi la formula diventa la seguente:
(350/4988) x 100 = 7,02%
Puoi facilmente notare che si tratta di un valore quasi identico a quello trovato all’inizio dei nostri calcoli. Dunque al risultato ottenuto senza applicare il Teorema di Pitagora. Questo scarto è di fatto insignificante. Questo significa che la precisione matematica non è necessaria, quando ti chiedi come calcolare la pendenza di una salita.Risulta essere decisamente più veloce applicare la formula iniziale, rispetto a quella del Teorema di Pitagora. Questo perché la discrepanza è davvero minima. Nonostante ciò, era giusto capire come ottenere il calcolo della pendenza con esattezza matematica.
Conclusioni
Vogliamo chiudere dandoti un’idea delle difficoltà delle varie pendenze
1-3% – salita leggera e poco impegnativa
4-6% – pendenza gestibile ma faticosa per ampie lunghezze
7-9% – pendenza impegnativa o molto impegnativa
10-15% – pendenza estremamente impegnativa
16% e oltre – pendenza impegnativa anche per i ciclisti più esperti
Il calcolo della pendenza di una salita può quindi essere utile in diverse situazioni.
